Sensor - ADXL345 - 3-Assige versnellingsmeter

Hardware

ADXL345 is een klein, laag vermogen, 3-assige versnellingsmeter met een hoge resolutie (13-bit) meting tot ± 16 g. Digitale uitgang van gegevens is opgemaakt als 16-bit. Uit te lezen via SPI of I2C.
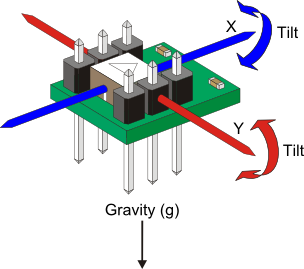
Voor het meten van: statische (tilt) en dynamische (bewegingen/schokken) versnelling en detectie van: tap, dubbel tap, vrije val en inactief, het wordt in veel apparaten toegepast, waaronder in mobiele telefoons en tablets (voor schermrotatie e.d.)

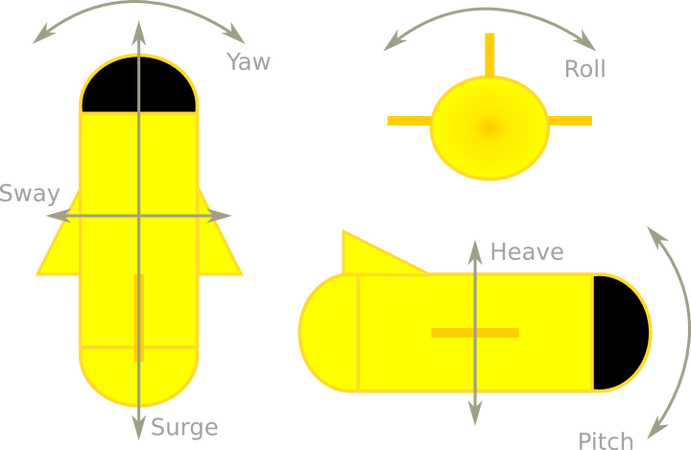
Accelerometers are devices that are capable of measuring the acceleration they experience relative to free-fall, the same acceleration living beings feel. As a consequence, accelerometers are incapable of measuring the acceleration of gravity, but can be used to measure the upwards acceleration that counters gravity when at rest. This acceleration is measured as $1g$ on the z-axis, when both pitch and roll angles are zero, but when the sensor is tilted either the x-axis or the y-axis experiences a component of the upward acceleration, whose magnitude depends on the tilt angle.

PITCH & ROLL ESTIMATION

Obtaining the pitch and roll angles is then a matter of being able to read the accelerometer, convert these readings to the g unit (1g = 9.8 m/s²), and apply the corresponding equations. The process of obtaining and converting the accelerometer readings depends on the accelerometer you are using, in my case, the ADXL345 in its basic configuration, provides 10-bit resolution for ±2g, but has several other ranges (±2g, ±4g, ±8g, ±16g) and resolutions (from 10 to 13 bits depending on the range) . Generalizing, the formula used to calculate the acceleration from the accelerometer readings is:

$G_{Accel} = Raw_{Accel} \cdot \dfrac{Range}{2^{Resolution - 1}}$

Once we have the correct acceleration components, we can proceed to calculate the different angles using the following equations:

$pitch = \arctan{\left(\dfrac{G_y}{\sqrt{G_{x}^2 + G_{z}^2}}\right)}$ $roll =\arctan{\left( \dfrac{-G_x}{ G_{z}}\right)}$

For more information about where these equations come from, you can read the documentation I include at the end of this post. As you can see, the denominator of the pitch equation is defined to be always positive, so the equation itself only provides $[-90, 90]$ range, which is exactly what is expected for the pitch angle. In contrast, the roll equation provides $[-180, 180]$ range. It is important to take into account that when the pitch angle is 90º, the surge axis (roll) is directly aligned with the gravity vector, thus we cannot measure the roll angle anymore, this is what is called Gimbal Lock.

Also, be aware that the roll equation is undefined when both $G_x$ and $G_z$ are equal to zero, and that for each possible value of the calculation done inside the arctan function there are two valid solutions, not only on the roll but also on the pitch equation. These problems can be easily solved in code by using the function atan2, which eliminates the angle calculation ambiguity by taking into account the quadrant.

REMOVING SHORT-TERM FLUCTUATIONS USING A LOW-PASS FILTER

At this point we already have a fully functional pitch & roll estimation system, but if we experiment with it we will discover that the readings fluctuate quite a bit and this may be very annoying for some applications. Removing these short-term fluctuations can be achieved by means of what is called a Low-Pass filter. This type of filter attenuates the higher frequencies of the signal, thus providing a smoother reading. The Low-Pass filter is easily implemented by using the following equation:

$y_{t} = \alpha \cdot x_{t} + (1 - \alpha) \cdot y_{t - 1}$

Where $y_t$ is our filtered signal, $y_{t-1}$ the previous filtered signal, $x_t$ the accelerometer reading and $\alpha$ the smoothing factor. It probably may seem obvious, but filtering should be done to the accelerometer readings before calculating the angles, instead of to the angles themselves. Regarding the smoothing factor, the lower we set it, the more it will take for the angle to stabilize, so we should not set it too low because then we could lose real-time behaviour. With this I mean that the reading will not correspond to the real angle until it stabilizes, and this could take some time.

Bron: https://theccontinuum.com/2012/09/24/arduino-imu-pitch-roll-from-accelerometer/

Pinout

Pin:	Functie:
1	SCL (serial clock)
2	SDA (serial data)
3	SD0 (serial data output)
4	INT1
5	INT2
6	CS (Chip Select)
7	VCC 3.3v+
8	GND

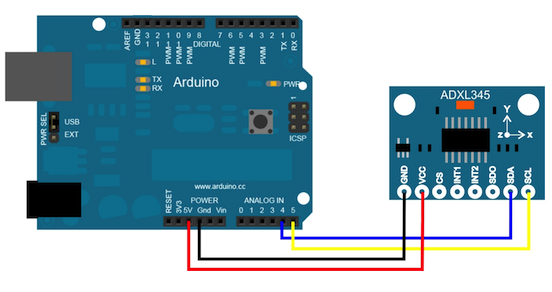
Arduino

Sluit de sensor aan volgens onderstaand overzicht:

Arduino pin:	ADXL345 pin:
A4	SDA (serial data)
A5	SCL (serial clock)
3.3v+	VCC 3.3v+
GND	GND

Script

Sluit de Accelerometer module aan zoals hierboven aangegeven.

#include <Wire.h>
#define DEVICE (0x53) // Device address as specified in data sheet
byte _buff[6];
char POWER_CTL = 0x2D;    //Power Control Register
char DATA_FORMAT = 0x31;
char DATAX0 = 0x32;    //X-Axis Data 0
char DATAX1 = 0x33;    //X-Axis Data 1
char DATAY0 = 0x34;    //Y-Axis Data 0
char DATAY1 = 0x35;    //Y-Axis Data 1
char DATAZ0 = 0x36;    //Z-Axis Data 0
char DATAZ1 = 0x37;    //Z-Axis Data 1

void setup() {
  Wire.begin(); // join i2c bus (address optional for master)
  Serial.begin(9600); // start serial for output. Make sure you set your Serial Monitor to the same!
  Serial.print("init");
  //Put the ADXL345 into +/- 4G range by writing the value 0x01 to the DATA_FORMAT register.
  writeTo(DATA_FORMAT, 0x01);
  //Put the ADXL345 into Measurement Mode by writing 0x08 to the POWER_CTL register.
  writeTo(POWER_CTL, 0x08);
}

void loop() {
  readAccel(); // read the x/y/z tilt
  delay(50); // only read every 0,5 seconds
}

void readAccel() {
  uint8_t howManyBytesToRead = 6;
  readFrom( DATAX0, howManyBytesToRead, _buff); //read the acceleration data from the ADXL345
  // each axis reading comes in 10 bit resolution, ie 2 bytes. Least Significat Byte first!!
  // thus we are converting both bytes in to one int
  int x = (((int)_buff[1]) << 8) | _buff[0];
  int y = (((int)_buff[3]) << 8) | _buff[2];
  int z = (((int)_buff[5]) << 8) | _buff[4];
  Serial.print("x: ");
  Serial.print( x );
  Serial.print(" y: ");
  Serial.print( y );
  Serial.print(" z: ");
  Serial.println( z );
}

void writeTo(byte address, byte val) {
  Wire.beginTransmission(DEVICE); // start transmission to device
  Wire.write(address); // send register address
  Wire.write(val); // send value to write
  Wire.endTransmission(); // end transmission
}
  
// Reads num bytes starting from address register on device in to _buff array
void readFrom(byte address, int num, byte _buff[]) {
  Wire.beginTransmission(DEVICE); // start transmission to device
  Wire.write(address); // sends address to read from
  Wire.endTransmission(); // end transmission
  Wire.beginTransmission(DEVICE); // start transmission to device
  Wire.requestFrom(DEVICE, num); // request 6 bytes from device
  int i = 0;
  while(Wire.available()) {// device may send less than requested (abnormal)
    _buff[i] = Wire.read(); // receive a byte
    i++;
    }
  Wire.endTransmission(); // end transmission
}

#include <Wire.h>

#define DEVICE (0x53) // Device address as specified in data sheet

byte _buff[6];

char POWER_CTL = 0x2D; //Power Control Register

char DATA_FORMAT = 0x31;

char DATAX0 = 0x32; //X-Axis Data 0

char DATAX1 = 0x33; //X-Axis Data 1

char DATAY0 = 0x34; //Y-Axis Data 0

char DATAY1 = 0x35; //Y-Axis Data 1

char DATAZ0 = 0x36; //Z-Axis Data 0

char DATAZ1 = 0x37; //Z-Axis Data 1

void setup() {

Wire.begin(); // join i2c bus (address optional for master)

Serial.begin(9600); // start serial for output. Make sure you set your Serial Monitor to the same!

Serial.print("init");

//Put the ADXL345 into +/- 4G range by writing the value 0x01 to the DATA_FORMAT register.

writeTo(DATA_FORMAT, 0x01);

//Put the ADXL345 into Measurement Mode by writing 0x08 to the POWER_CTL register.

writeTo(POWER_CTL, 0x08);

}

void loop() {

readAccel(); // read the x/y/z tilt

delay(50); // only read every 0,5 seconds

}

void readAccel() {

uint8_t howManyBytesToRead = 6;

readFrom( DATAX0, howManyBytesToRead, _buff); //read the acceleration data from the ADXL345

// each axis reading comes in 10 bit resolution, ie 2 bytes. Least Significat Byte first!!

// thus we are converting both bytes in to one int

int x = (((int)_buff[1]) << 8) | _buff[0];

int y = (((int)_buff[3]) << 8) | _buff[2];

int z = (((int)_buff[5]) << 8) | _buff[4];

Serial.print("x: ");

Serial.print( x );

Serial.print(" y: ");

Serial.print( y );

Serial.print(" z: ");

Serial.println( z );

}

void writeTo(byte address, byte val) {

Wire.beginTransmission(DEVICE); // start transmission to device

Wire.write(address); // send register address

Wire.write(val); // send value to write

Wire.endTransmission(); // end transmission

}

// Reads num bytes starting from address register on device in to _buff array

void readFrom(byte address, int num, byte _buff[]) {

Wire.beginTransmission(DEVICE); // start transmission to device

Wire.write(address); // sends address to read from

Wire.endTransmission(); // end transmission

Wire.beginTransmission(DEVICE); // start transmission to device

Wire.requestFrom(DEVICE, num); // request 6 bytes from device

int i = 0;

while(Wire.available()) {// device may send less than requested (abnormal)

_buff[i] = Wire.read(); // receive a byte

i++;

}

Wire.endTransmission(); // end transmission

}

Het resultaat

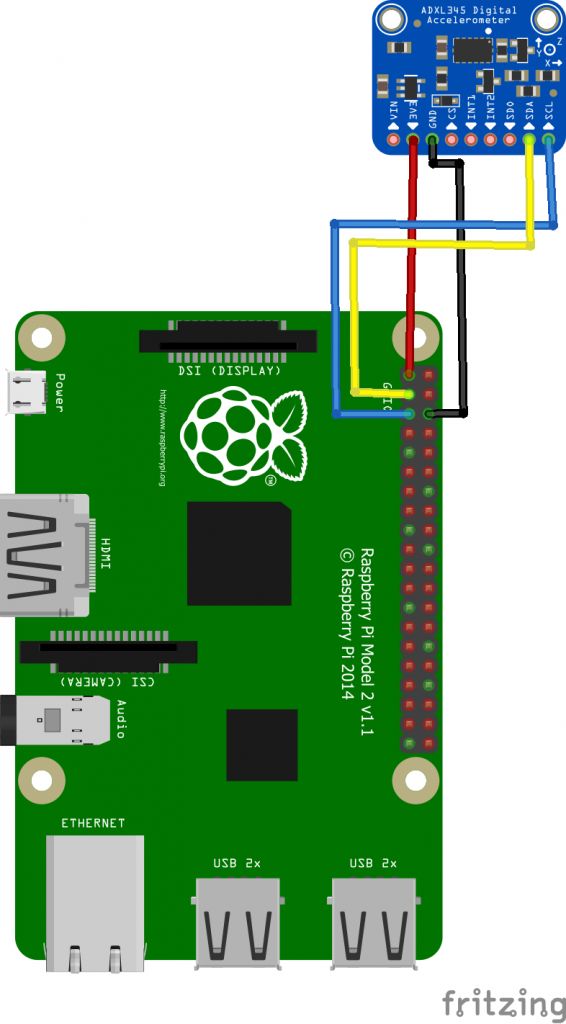
Raspberry Pi

Connect the sensor like:

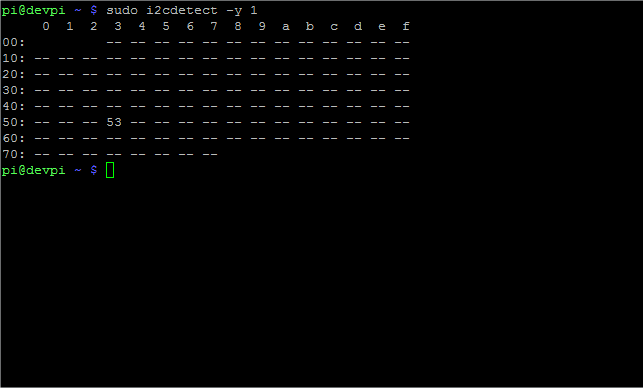
The I2C ADXL module will be found with adress 0x53:

Script

Use the adafruit library to easy read out your sensor.

# Simple demo of of the ADXL345 accelerometer library.  Will print the X, Y, Z
# axis acceleration values every half second.
# Author: Tony DiCola
# License: Public Domain
import time

# Import the ADXL345 module.
import Adafruit_ADXL345

# Create an ADXL345 instance.
accel = Adafruit_ADXL345.ADXL345()

# Alternatively you can specify the device address and I2C bus with parameters:
#accel = Adafruit_ADXL345.ADXL345(address=0x54, busnum=2)

# You can optionally change the range to one of:
#  - ADXL345_RANGE_2_G   = +/-2G (default)
#  - ADXL345_RANGE_4_G   = +/-4G
#  - ADXL345_RANGE_8_G   = +/-8G
#  - ADXL345_RANGE_16_G  = +/-16G
# For example to set to +/- 16G:
#accel.set_range(Adafruit_ADXL345.ADXL345_RANGE_16_G)

# Or change the data rate to one of:
#  - ADXL345_DATARATE_0_10_HZ = 0.1 hz
#  - ADXL345_DATARATE_0_20_HZ = 0.2 hz
#  - ADXL345_DATARATE_0_39_HZ = 0.39 hz
#  - ADXL345_DATARATE_0_78_HZ = 0.78 hz
#  - ADXL345_DATARATE_1_56_HZ = 1.56 hz
#  - ADXL345_DATARATE_3_13_HZ = 3.13 hz
#  - ADXL345_DATARATE_6_25HZ  = 6.25 hz
#  - ADXL345_DATARATE_12_5_HZ = 12.5 hz
#  - ADXL345_DATARATE_25_HZ   = 25 hz
#  - ADXL345_DATARATE_50_HZ   = 50 hz
#  - ADXL345_DATARATE_100_HZ  = 100 hz (default)
#  - ADXL345_DATARATE_200_HZ  = 200 hz
#  - ADXL345_DATARATE_400_HZ  = 400 hz
#  - ADXL345_DATARATE_800_HZ  = 800 hz
#  - ADXL345_DATARATE_1600_HZ = 1600 hz
#  - ADXL345_DATARATE_3200_HZ = 3200 hz
# For example to set to 6.25 hz:
#accel.set_data_rate(Adafruit_ADXL345.ADXL345_DATARATE_6_25HZ)

print('Printing X, Y, Z axis values, press Ctrl-C to quit...')
while True:
    # Read the X, Y, Z axis acceleration values and print them.
    x, y, z = accel.read()
    print('X={0}, Y={1}, Z={2}'.format(x, y, z))
    # Wait half a second and repeat.
    time.sleep(0.5)

# Simple demo of of the ADXL345 accelerometer library. Will print the X, Y, Z

# axis acceleration values every half second.

# Author: Tony DiCola

# License: Public Domain

import time

# Import the ADXL345 module.

import Adafruit_ADXL345

# Create an ADXL345 instance.

accel = Adafruit_ADXL345.ADXL345()

# Alternatively you can specify the device address and I2C bus with parameters:

#accel = Adafruit_ADXL345.ADXL345(address=0x54, busnum=2)

# You can optionally change the range to one of:

# - ADXL345_RANGE_2_G = +/-2G (default)

# - ADXL345_RANGE_4_G = +/-4G

# - ADXL345_RANGE_8_G = +/-8G

# - ADXL345_RANGE_16_G = +/-16G

# For example to set to +/- 16G:

#accel.set_range(Adafruit_ADXL345.ADXL345_RANGE_16_G)

# Or change the data rate to one of:

# - ADXL345_DATARATE_0_10_HZ = 0.1 hz

# - ADXL345_DATARATE_0_20_HZ = 0.2 hz

# - ADXL345_DATARATE_0_39_HZ = 0.39 hz

# - ADXL345_DATARATE_0_78_HZ = 0.78 hz

# - ADXL345_DATARATE_1_56_HZ = 1.56 hz

# - ADXL345_DATARATE_3_13_HZ = 3.13 hz

# - ADXL345_DATARATE_6_25HZ = 6.25 hz

# - ADXL345_DATARATE_12_5_HZ = 12.5 hz

# - ADXL345_DATARATE_25_HZ = 25 hz

# - ADXL345_DATARATE_50_HZ = 50 hz

# - ADXL345_DATARATE_100_HZ = 100 hz (default)

# - ADXL345_DATARATE_200_HZ = 200 hz

# - ADXL345_DATARATE_400_HZ = 400 hz

# - ADXL345_DATARATE_800_HZ = 800 hz

# - ADXL345_DATARATE_1600_HZ = 1600 hz

# - ADXL345_DATARATE_3200_HZ = 3200 hz

# For example to set to 6.25 hz:

#accel.set_data_rate(Adafruit_ADXL345.ADXL345_DATARATE_6_25HZ)

print('Printing X, Y, Z axis values, press Ctrl-C to quit...')

while True:

# Read the X, Y, Z axis acceleration values and print them.

x, y, z = accel.read()

print('X={0}, Y={1}, Z={2}'.format(x, y, z))

# Wait half a second and repeat.

time.sleep(0.5)

Raspberry Pi Library

Python code to use the ADXL345 triple-axis accelerometer over I2C with a Raspberry Pi or BeagleBone Black.

Installation

To install the library from source (recommended) run the following commands on a Raspberry Pi or other Debian-based OS system:

sudo apt-get install git build-essential python-dev

cd ~

git clone https://github.com/adafruit/Adafruit_Python_ADXL345.git

cd Adafruit_Python_ADXL345

sudo python setup.py install

Alternatively you can install from pip with:

1 2	sudo pip install adafruit-adxl345

Note that the pip install method won’t install the example code.

Download github: https://github.com/adafruit/Adafruit_Python_ADXL345

Adafruit_Python_ADXL345-master

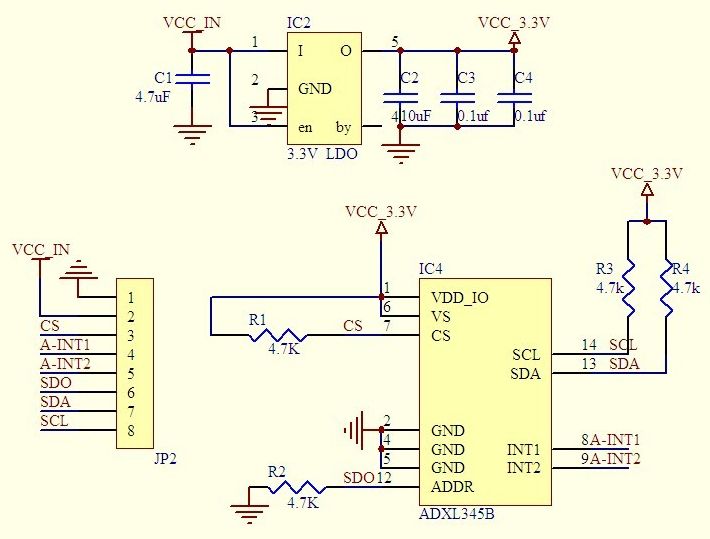
Schema

Teardown

GEEN GEGEVENS

Datasheet

ADXL345 Digital Accelerometer datasheet rev.E (analog devices)

ADXL345 Digital Accelerometer (adafruit learning system)

Fritzing

GEEN GEGEVENS

Downloads

GEEN GEGEVENS

Zoeken

Sensor – ADXL345 – 3-Assige versnellingsmeter

Hardware

PITCH & ROLL ESTIMATION

REMOVING SHORT-TERM FLUCTUATIONS USING A LOW-PASS FILTER

Pinout

Arduino

Script

Het resultaat

Raspberry Pi

Script

Raspberry Pi Library

Installation

Schema

Teardown

Datasheet

Fritzing

Downloads