Wat is Signed/Unsinged Integer 16/32/64-bit?

Je hebt er wel eens van gehoord die signed en unsigned integers, maar wat is dit nu precies?, en hoe kan je hiermee rekenen?

Laten we bij het begin beginnen

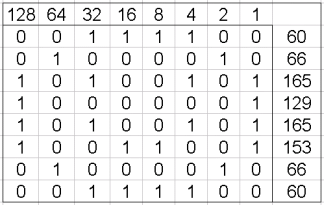
Neem bijvoorbeeld 1 byte, deze is opgebouwd uit 8 bits van 1’en en/of 0’en, bijvoorbeeld: 00010011 (= getal: 19), deze byte (oftewel bitreeks) kan een (decimaal) getal vertegenwoordigen van 0 tot 255 (256), zie de voorbeelden hier:

Het lezen en omrekenen van de bitreeks op deze manier is UNSIGNED, omdat het getal ALTIJD POSITIEF is, hoeft er geen bitje aan te geven of het getal positief of negatief is.

SIGNED INTEGERS (oftewel “binary16”)

In het voorbeeld hierboven kan een unsigned integer (meestal 1 byte/8 bits) maar een positief getal aangeven van 0 tot 255 (256).
Bij gebruikt van 2 bytes (16 bits) en met zgn “floating points” te werken zou je theoretisch een waarde kunnen halen van 256 x 256 (65536), Maar de maximaal haalbare waarde is (2−2−10) × 215 = 65504.

SIGNED integers kunnen POSITIEF of NEGATIEF zijn, vandaar “signed”.

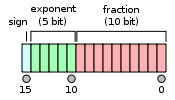
De opbouw van een “signed integer” (16-bits) (2 bytes) is als volgt opgebouwd:

1) Sign bit: 1 bit
2) Exponent width: 5 bits
3) Significand precision: 11 bits (10 werkelijk opgeslagen)

bij 32-bit:
1) Sign bit: 1 bit
2) Exponent width: 8 bits
3) Significand precision: 24 bits (23 werkelijk opgeslagen)

bij 64-bit:
1) Sign bit: 1 bit
2) Exponent width: 11 bits
3) Significand precision: 53 bits (52 werkelijk opgeslagen)

Wat houd dit in?:
1) de “sign” bit geeft aan of het (decimale) getal positief (0) of negatief (1) is.
2) “Exponent” oftewel het aantal machten dat over de “Significand” moet worden gemaakt.
3) “Significand”, het getal dat met het aantal machten moet worden verrrekend.

BIAS?
De “BIAS” is een getal dat je van het “Exponent” moet aftrekken voordat je hiermee gaat rekenen!, het BIAS getal is afhankelijk van het aantal bits aan “Exponenten”

De formule voor het berekenen van BIAS is als volgt: 2^(n-1) – 1

Als voorbeeld de berekening van de BIAS bij een 16-bit reeks (n = aantal “Exponent” bits):
stap 1) Bias = 2^(5-1) – 1
stap 2) Bias = 2^4 – 1
stap 3) Bias = 16 – 1
stap 4) Bias = 15

bij 32-bit:
stap 1) Bias = 2^(8-1) – 1
stap 2) Bias = 2^7 – 1
stap 3) Bias = 128 – 1
stap 4) Bias = 127

bij 64-bit:
stap 1) Bias = 2^(11-1) – 1
stap 2) Bias = 2^10 – 1
stap 3) Bias = 1024 – 1
stap 4) Bias = 1023

Voorbeelden om byte’s omzetten naar 16-bit/32-bit integers

Voorbeeld (16-bit):
Hex waarde: 3C00 (2 bytes)
Binaire waarde: 0011 1100 0000 0000 (16 bit)
Opbouw signed: 0 | 01111 | 0000000000 (16 bit)
Sign (het eerste bitje van links): = 0 (positief)
Exponent (5 bits): 01111 = 15 (decimal) —> 15 – 15 (bias) = 0 ; 2 ^ 0 = 1
Significand (10 bits): 0000000000 (10 bits) = 0 (decimal) + 1 (implicit bit) = 1

De waarde is dan “Exponent” x “Significand” = 1 x 1 = 1

Voorbeeld (16-bit):
Hex waarde: 7BFF (2 bytes)
Binaire waarde: 0111101111111111 (16 bit)
Opbouw signed: 0 | 11110 | 1111111111 (16 bit)
Sign (het eerste bitje van links): 0 (positief)
Exponent (5 bits): 11110 = 30 (decimal) —> 30 – 15 (bias) = 15 —> 2 ^ 15 = 32768
Significand (10 bits): 1111111111 = 1023 (decimal) —> 1023 / 1024 (bits te schuiven) = 0,9990234375 –> +1 (implicit bit) = 1,9990234375

De waarde is dan “Exponent” x “Significand” = 32768 x 1,9990234375 = 65504

Voorbeeld (16-bit):
Hex waarde: 50DE (2 bytes)
Binaire waarde: 0101 0000 1101 1110 (16 bit)
Opbouw signed: 0 | 10100 | 0011011110 (16 bit)
Sign (het eerste bitje van links): 0 (positief)
Exponent (5 bits): 10100 = 20 (decimal) —> 20 – 15 (bias) = 5 —> 2 ^ 5 = 32
Significand (10 bits): 0011011110 = 222 (decimal) —> 222 / 1024 (bits te schuiven) = 0,216796875 –> +1 (implicit bit) = 1,216796875

De waarde is dan “Exponent” x “Significand” = 32 x 1,216796875 = 38,9375

Voorbeeld (32-bit):
Hex waarde: BDAE147B (4 bytes)
Binaire waarde: 1011 1101 1010 1110 0001 0100 0111 1011 (32 bit)
Opbouw signed: 1 | 01111011 | 01011100001010001111011 (32 bit)
Sign (het eerste bitje van links): 1 (negatief)
Exponent (8 bits): 01111011 = 123 (decimal) —> 123 – 127 (bias) = -4 —> 2 ^ -4 = 0,0625
Significand (23 bits): 01011100001010001111011 = 3.019.899 (decimal) —> 3.019.899 / 8.388.608 (bits te schuiven) = 0,36000001430511474609375 –> +1 (implicit bit) = 1,36000001430511474609375

De waarde is dan -1 x “Exponent” x “Significand” = -1 x 0,0625 x 1,36000001430511474609375 = -0,085

In formuleform:
Gebruik de formule (-1 ^ Sign) * (2 ^ Exponent) * Significand om de waarde te berekenen:
stap 1) (-1 ^ -1) * (2 ^ Exponent) * Significand
stap 2) -1 * (2 ^ Exponent) * Significand
stap 3) -1 * (2 ^ -4) * Significand
stap 4) -1 * 0,0625 * Significand
stap 5) -1 * 0,0625 * 1.36000001430511474609375
stap 6) -1 * 0.085000000894069671630859375
antwoord) -0.085000000894069671630859375 (oftewel -0,085)

Het omgekeerde process:

+ to find the exponent, floor(log2(decimal number))

so, floor(log2(65504)) == floor(15.999295) == 15

+ find the significand
2^15 = 32768 ==> 65504/32768 = 1.9990234

+ subtract 1, then multiply by 1024
(1.9990234 – 1) * 1024 = 1023

+ encode significand result into binary
1023 = 0b1111111111

+ bias the exponent (i.e. add 15), then convert to signed two’s complement integer binary
15 + 15 = 30 ==> 0b11110

+ concatenate sign, bias exponent, significant
0|11110|11111111111

+ convert to hex
0111 1011 1111 1111 ==> 0x7BFF

Bronnen: jul.rustedlogic.net / wikipedia